The goal of my research program is to understand the cognitive and developmental factors that support our ability to engage in proportional reasoning, as well as what factors lead us astray. Flexibly reasoning about quantities in terms of both their absolute amount and in relation to other quantities is an important feature of human cognition. For example, imagine you are buying a bag of apples to make a pie. You inspect a bag at the store and see 8 good apples, exactly the number you need. This absolute information about the number of apples is sufficient to meet your current goal. However, whether those 8 good apples are in a small bag, making up 80% of the apples, or a large bag, making up 25% of the apples, provides additional information. You might use this ratio of good vs. rotten apples to make inferences about the quality of the bag or the expected good vs. rotten apple distribution in other bags of various sizes. As this example illustrates, we are often presented with information about absolute features (i.e., 8 apples) and the relations among them (i.e., 80% vs. 25%). I use developmental, experimental, and computational methods to investigate how we reason about the relations between quantities, including how we flexibly navigate different pieces of quantitative information and what cognitive and developmental factors impact this behavior. This work is currently funded by a K99/R00 Pathway to Independence Award from the NICHD.
By taking a basic-science approach to addressing the development of humans' mathematical reasoning, my research addresses questions at the intersection of cognitive, developmental, and educational science.
By taking a basic-science approach to addressing the development of humans' mathematical reasoning, my research addresses questions at the intersection of cognitive, developmental, and educational science.
Highlights from some current lines of work:
How does proportional reasoning develop through childhood?
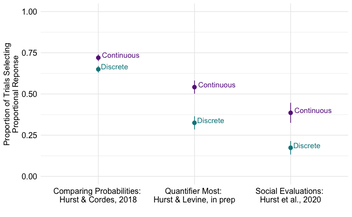
Even before learning formal fractions, young children and infants have fairly surprising intuitions about probability and proportion. Yet, 6-year-old children also show systematic errors in how they use proportion information: when the number of items is inconsistent with the overall proportion (e.g., 3/4 vs. 5/9 where 3 < 5 but 3/4 > 5/9), children tend to make mistakes because they rely more on the number of items than the proportion (Hurst & Cordes, 2018; Dev Psych).
In order to better understand children's intuitions, I have several studies investigating how children's proportional reasoning varies across contexts, what factors can change children's proportional reasoning strategies, and the development of children's errors. Overall, my work suggests that perceptual factors that impact children's tendency to rely on proportional information may be fairly general. That is, when the quantities are presented discretely and divided up children are less likely to rely on proportion than when the quantities are presented continuously and undivided - and this is true in a range of contexts (see Figure), including probabilities (Hurst & Cordes, 2018), their understanding of the quantifier most (Hurst & Levine, in prep), and their social evaluations of others based on how they shared resources (Hurst et al., 2020). This pervasive phenomenon has led to a productive and important research program about the origins of and cognitive processes that give rise to this error, and how to help children overcome it. In ongoing and future work, I'm excited about new projects investigating infants proportional reasoning and how their ability to track proportional information might (or might not!) be similarly dependent on the perceptual format of the display.
Some representative publications about this work:
Hurst, M. A., Shaw, A., Chernyak, N., & Levine, S.C. (2020). Giving a Larger Amount or a Larger Proportion: Stimulus Format Impacts Children’s Social Evaluations, In Press at Developmental Psychology. [Preregistration, data, materials, and manuscript available at: https://osf.io/5g34d/]
Hurst, M. A., & Cordes, S. (2019). Talking about proportion: Fraction labels impact numerical interference in non-symbolic proportional reasoning, Developmental Science, 22(4). doi: 10.1111/desc.12790 [Data and Materials available at: https://osf.io/z4xhv/]
Hurst, M. A., & Cordes, S. (2018). Attending to Relations: Proportional reasoning in 3- to 6-year-old children, Developmental Psychology, 54(3), 428-439. doi: 10.1037/dev0000440
In order to better understand children's intuitions, I have several studies investigating how children's proportional reasoning varies across contexts, what factors can change children's proportional reasoning strategies, and the development of children's errors. Overall, my work suggests that perceptual factors that impact children's tendency to rely on proportional information may be fairly general. That is, when the quantities are presented discretely and divided up children are less likely to rely on proportion than when the quantities are presented continuously and undivided - and this is true in a range of contexts (see Figure), including probabilities (Hurst & Cordes, 2018), their understanding of the quantifier most (Hurst & Levine, in prep), and their social evaluations of others based on how they shared resources (Hurst et al., 2020). This pervasive phenomenon has led to a productive and important research program about the origins of and cognitive processes that give rise to this error, and how to help children overcome it. In ongoing and future work, I'm excited about new projects investigating infants proportional reasoning and how their ability to track proportional information might (or might not!) be similarly dependent on the perceptual format of the display.
Some representative publications about this work:
Hurst, M. A., Shaw, A., Chernyak, N., & Levine, S.C. (2020). Giving a Larger Amount or a Larger Proportion: Stimulus Format Impacts Children’s Social Evaluations, In Press at Developmental Psychology. [Preregistration, data, materials, and manuscript available at: https://osf.io/5g34d/]
Hurst, M. A., & Cordes, S. (2019). Talking about proportion: Fraction labels impact numerical interference in non-symbolic proportional reasoning, Developmental Science, 22(4). doi: 10.1111/desc.12790 [Data and Materials available at: https://osf.io/z4xhv/]
Hurst, M. A., & Cordes, S. (2018). Attending to Relations: Proportional reasoning in 3- to 6-year-old children, Developmental Psychology, 54(3), 428-439. doi: 10.1037/dev0000440
How is proportion represented?
Proportional information is unique in that it is simultaneously a relation between magnitudes (e.g., 3 out of 4) and a magnitude in and of itself (e.g., 0.75), which means there are many possible approaches to encoding and representing this information. For example, when looking at an array of red and blue dots, one could encode the relation ¾ by looking at the number of red dots and the total, the number of red dots and blue dots, or by directly perceiving the relation without encoding the identity of the absolute amounts. In prior work, I have found that not all these pieces of quantitative information are equally weighted during this process and the representational format impacts reasoning (Hurst et al., 2020, Dev Psych; Hurst, Boyer, & Cordes, 2021, JEP: LMC). As part of my K99 award, I am using a computational modeling approach to test theoretical predictions about how quantitative information in a display is used to make proportional judgements. That is, how much does performance depend on each component of the display – the numerator amount, the denominator amount, and the ratio magnitude? Most importantly, I am using the same modeling approach to directly compare data from judgements of discrete proportional information and continuous proportional information to provide a formal test of how human cognitive processing differs across these two contexts. In preliminary analyses, I have explored how different quantitative features differentially impact adults’ decisions and have found that proportional magnitude has a significantly larger effect on performance for continuous stimuli, whereas the numerator magnitude has a larger effect on performance for discrete stimuli. Together, this suggests that when encoding and using proportional information, adults weigh visually available quantitative information differently based on the perceptual characteristics of the display. This is a promising approach for developing a formal model of how quantitative dimensions are processed and combined to make decisions with proportional information.
Some representative publications about this work:
Hurst, M. A., Boyer, T. W., & Cordes, S. (2021). Spontaneous and Directed Attention to Number and Proportion, Journal of Experimental Psychology: Learning, Memory, and Cognition. Accepted July 2021.
Some representative publications about this work:
Hurst, M. A., Boyer, T. W., & Cordes, S. (2021). Spontaneous and Directed Attention to Number and Proportion, Journal of Experimental Psychology: Learning, Memory, and Cognition. Accepted July 2021.
How do different formal representations impact fraction learning?
Learning fractions is extremely difficult for many children (and adults!), but recent work by me and by others suggests that learning fractions is extremely important for later math learning, especially algebra.
One of the things that makes learning about fractions so difficult is the many ways it can be talked about and represented. By investigating how these different representations impact people's thinking, we can learn more about how our minds mentally represent information and communicate it to others. Also, if we have a better understanding of how children and adults think about fractions, across different representations, we may be able to construct curricula that better match how children think and learn.
In my work in particular, I'm interested in how different aspects of fraction information (for example: ratio, proportion, part-whole relations, magnitude information, etc.) are understood using different notations and representations (for example: fractions, decimals, pie charts, number lines, discrete items, etc.). In particular, I'm interested in which notations/representations may be best matched for reasoning about specific types of fraction concepts, and not as good others. For example, some recent research suggests that fractions may be particularly difficult for magnitude information (Hurst & Cordes, 2016, JEP:HPP; 2018, JECP) and that people may be more likely to treat area models in a way that preserves part-whole information in addition to magnitude (Hurst, Massaro, & Cordes, 2020; Hurst, Santry, Relander, & Cordes, in prep).
In future and on-going work, I'm very interested in taking what we learn about young children intuitions and using them for formal fraction learning in a way that can take advantage of children's existing knowledge.
Some representative publications about this work:
Hurst, M., & Cordes, S. (2016). Rational Number Comparison Across Notation: Fractions, Decimals, and Whole Numbers. Journal of Experimental Psychology: Human Perception and Performance, 42(2), 281-293. doi: 10.1037/xhp0000140
Hurst, M. A., & Cordes, S. (2018). Children’s understanding of fraction and decimal symbolic magnitudes and its relationship to pre-algebra ability, Journal of Experimental Child Psychology, 168, 32-48. doi: 10.1016/j.jecp.2017.12.003.
One of the things that makes learning about fractions so difficult is the many ways it can be talked about and represented. By investigating how these different representations impact people's thinking, we can learn more about how our minds mentally represent information and communicate it to others. Also, if we have a better understanding of how children and adults think about fractions, across different representations, we may be able to construct curricula that better match how children think and learn.
In my work in particular, I'm interested in how different aspects of fraction information (for example: ratio, proportion, part-whole relations, magnitude information, etc.) are understood using different notations and representations (for example: fractions, decimals, pie charts, number lines, discrete items, etc.). In particular, I'm interested in which notations/representations may be best matched for reasoning about specific types of fraction concepts, and not as good others. For example, some recent research suggests that fractions may be particularly difficult for magnitude information (Hurst & Cordes, 2016, JEP:HPP; 2018, JECP) and that people may be more likely to treat area models in a way that preserves part-whole information in addition to magnitude (Hurst, Massaro, & Cordes, 2020; Hurst, Santry, Relander, & Cordes, in prep).
In future and on-going work, I'm very interested in taking what we learn about young children intuitions and using them for formal fraction learning in a way that can take advantage of children's existing knowledge.
Some representative publications about this work:
Hurst, M., & Cordes, S. (2016). Rational Number Comparison Across Notation: Fractions, Decimals, and Whole Numbers. Journal of Experimental Psychology: Human Perception and Performance, 42(2), 281-293. doi: 10.1037/xhp0000140
Hurst, M. A., & Cordes, S. (2018). Children’s understanding of fraction and decimal symbolic magnitudes and its relationship to pre-algebra ability, Journal of Experimental Child Psychology, 168, 32-48. doi: 10.1016/j.jecp.2017.12.003.
